Ebene Figuren: Unterschied zwischen den Versionen

Aus Grundschullernportal
Wechseln zu: Navigation, Suche
 
(14 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt)
Zeile 1: Zeile 1:
 
=== Ebene Figuren ===
 
=== Ebene Figuren ===
−
Um eine ebene Figur herzustellen, brauchst du mindestens drei Punkte, die du durch Strecken verbindest. Zum Beispiel kannst du mit den drei Punkten ein Dreieck bilden, mit vier Punkten ein Viereck. Die Anzahl der Punkte bestimmt also die Anzahl der Ecken. Die einzige ebene Figur, die keinen Punkt besitzt, ist der Kreis.  
+
Der Begriff '''"ebene Figuren"''' gehört zum mathematischen Themenbereich der '''Geometrie'''.
−
Im Gegensatz zu geometrischen Körpern haben ebene Figuren kein Volumen. Sie setzen sich aus einer Länge und einer Breite zusammen, sodass sie auf eine Fläche projizierbar sind. Das heißt sie sind zweidimensional. Würde man eine ebene Figur von der Fläche aus in die Höhe ziehen, würde daraus ein dreidimensionaler Körper (geometrischer Körper) entstehen.
+
 
 +
Um eine ebene Figur herzustellen, braucht man mindestens drei Eckpunkte, die durch Strecken verbunden werden. Zum Beispiel kann man mit den drei Eckpunkten ein Dreieck bilden, mit vier Eckpunkten ein Viereck. Die einzige ebene Figur, die keinen Eckpunkt besitzt, ist der Kreis.  
 +
Im Gegensatz zu [[Matheprojekte der Justus-Liebig-Universität Gießen für Grundschülerinnen und Grundschüler/Mathelexikon WiSe 16 17/Geometrische Körper|geometrischen Körpern]] haben ebene Figuren kein [[Matheprojekte der Justus-Liebig-Universität Gießen für Grundschülerinnen und Grundschüler/Mathelexikon WiSe 16 17/Volumen|Volumen]]. Sie setzen sich aus einer Länge und einer Breite zusammen. Das heißt sie sind zweidimensional. Würde man eine ebene Figur von der Fläche aus in die Höhe ziehen, würde daraus ein dreidimensionaler Körper (geometrischer Körper) entstehen.
 +
 
 
==== Beispiele ====
 
==== Beispiele ====
−
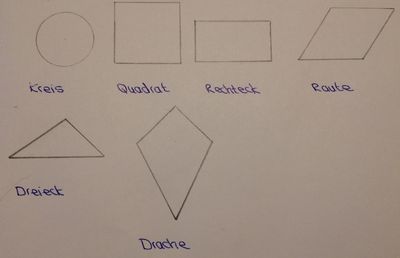
Es gibt verschiedene ebene Figuren. Die bekanntesten ebenen Figuren sind Rechteck, Quadrat, Raute, Quadrat, Raute, Drache, Dreieck, Kreis, Sechseck und Trapez.
+
Es gibt verschiedene ebene Figuren. Die bekanntesten ebenen Figuren sind [[Matheprojekte der Justus-Liebig-Universität Gießen für Grundschülerinnen und Grundschüler/Mathelexikon WiSe 16 17/Rechteck|Rechteck]], [[Matheprojekte der Justus-Liebig-Universität Gießen für Grundschülerinnen und Grundschüler/Mathelexikon WiSe 16 17/Quadrat|Quadrat]], [[Matheprojekte der Justus-Liebig-Universität Gießen für Grundschülerinnen und Grundschüler/Mathelexikon WiSe 16 17/Raute|Raute]], [[Matheprojekte der Justus-Liebig-Universität Gießen für Grundschülerinnen und Grundschüler/Mathelexikon WiSe 16 17/Drachen|Drache]], Dreieck, Kreis, Sechseck und Trapez.
−
[[File:Geometria 02.svg|left|Ebene Figuren|200px]]
+
 
−
==== Ebene Figuren im Alltag ====
+
[[File:Hexagonal tiling.svg|Sechsecke angeordnet in einer Parkettierung|200px]] [[Datei:Ebene Figuren.JPG|ebene Figuren|400px]]
−
Im Alltag gibt es kaum Beispiele für ebene Figuren, da die meisten Beispiele ein Volumen besitzen und deshalb geometrische Körper sind. Man kann jedoch sagen, dass verschiedene Gegenstände die Form einer ebenen Figur besitzen.
+
 
−
* Ein Fenster hat die Form eines Vierecks.
+
==== Alltagsbezug ====
−
* Eine Tür hat die Form eines Rechtecks.
+
Im Alltag gibt es viele Beispiele für ebene Figuren. Man kann ebene Figuren zum Beispiel als Seitenflächen von verschiedenen Gegenständen finden. Die Gegenstände selbst sind dabei keine ebenen Figuren, sie sind geometrische Körper.  
−
* Eine Uhr hat die Form eines Kreises.
+
* Ein Fenster sieht aus wie ein Viereck.
 +
* Eine Tür sieht aus wie ein Rechteck.
 +
* Eine Hauswand sieht aus wie ein Rechteck.
 +
* Eine Uhr sieht aus wie ein Kreis.
 +
* Eine Bienenwabe sieht aus wie ein Sechseck.
 +
* Ein Hausdach sieht aus wie ein Dreieck.

Aktuelle Version vom 28. Februar 2017, 17:41 Uhr

Ebene Figuren

Der Begriff "ebene Figuren" gehört zum mathematischen Themenbereich der Geometrie.

Um eine ebene Figur herzustellen, braucht man mindestens drei Eckpunkte, die durch Strecken verbunden werden. Zum Beispiel kann man mit den drei Eckpunkten ein Dreieck bilden, mit vier Eckpunkten ein Viereck. Die einzige ebene Figur, die keinen Eckpunkt besitzt, ist der Kreis. Im Gegensatz zu geometrischen Körpern haben ebene Figuren kein Volumen. Sie setzen sich aus einer Länge und einer Breite zusammen. Das heißt sie sind zweidimensional. Würde man eine ebene Figur von der Fläche aus in die Höhe ziehen, würde daraus ein dreidimensionaler Körper (geometrischer Körper) entstehen.

Beispiele

Es gibt verschiedene ebene Figuren. Die bekanntesten ebenen Figuren sind Rechteck, Quadrat, Raute, Drache, Dreieck, Kreis, Sechseck und Trapez.

Sechsecke angeordnet in einer Parkettierung ebene Figuren

Alltagsbezug

Im Alltag gibt es viele Beispiele für ebene Figuren. Man kann ebene Figuren zum Beispiel als Seitenflächen von verschiedenen Gegenständen finden. Die Gegenstände selbst sind dabei keine ebenen Figuren, sie sind geometrische Körper.

  • Ein Fenster sieht aus wie ein Viereck.
  • Eine Tür sieht aus wie ein Rechteck.
  • Eine Hauswand sieht aus wie ein Rechteck.
  • Eine Uhr sieht aus wie ein Kreis.
  • Eine Bienenwabe sieht aus wie ein Sechseck.
  • Ein Hausdach sieht aus wie ein Dreieck.
Von „https://alt.grundschullernportal.de/index.php?title=Matheprojekte_der_Justus-Liebig-Universität_Gießen_für_Grundschülerinnen_und_Grundschüler/Mathelexikon_WiSe_16_17/Ebene_Figuren&oldid=4679“