Rechteck: Unterschied zwischen den Versionen
| (21 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
==Definition== | ==Definition== | ||
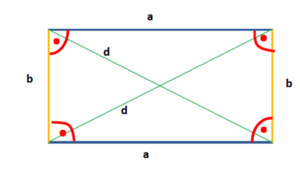
| − | Ein | + | Ein '''Rechteck''' ist eine [[Matheprojekte der Justus-Liebig-Universität Gießen für Grundschülerinnen und Grundschüler/Mathelexikon WiSe 16 17/Ebene Figuren|ebene Figur]]. Es ist ein [[Matheprojekte der Justus-Liebig-Universität Gießen für Grundschülerinnen und Grundschüler/Mathelexikon WiSe 16 17/Viereck|Viereck]] mit parallelen Gegenseiten und vier rechten [[Matheprojekte der Justus-Liebig-Universität Gießen für Grundschülerinnen und Grundschüler/Mathelexikon WiSe 16 17/Winkel|Winkeln]]. Die Winkelsumme der Innenwinkel beträgt also 360°. Die gegenüberliegenden Seiten eines Rechtecks sind jeweils gleich lang. Die beiden längeren Seiten bezeichnet man als [[Matheprojekte der Justus-Liebig-Universität Gießen für Grundschülerinnen und Grundschüler/Mathelexikon WiSe 16 17/Länge|Länge]] a des Rechtecks. Die beiden kürzeren Seiten werden als Breite b des Rechtecks bezeichnet. Auch die Diagonalen d in einem Rechteck sind gleich lang und halbieren sich gegenseitig. |
| − | [[Datei: | + | [[Datei:Rechteck.PNG|miniatur|zentriert|Rechteck mit Länge a und Breite b; gleichlangen und parallelen Gegenseiten; gleichlangen Diagonalen d, welche sich gegenseitig halbieren und 4 rechten Innenwinkeln]]<br /> |
| − | + | ||
| − | + | ||
| − | + | ||
==Formel für den Umfang== | ==Formel für den Umfang== | ||
| − | Der Umfang eines Rechtecks lässt sich | + | Der [[Matheprojekte der Justus-Liebig-Universität Gießen für Grundschülerinnen und Grundschüler/Mathelexikon WiSe 16 17/Umfang|Umfang]] eines Rechtecks lässt sich berechnen, indem man die Seitenlängen aller vier Seiten addiert. Da jeweils zwei Seiten eines Rechtecks gleich lang sind, kann man diese mit „2“ multiplizieren. Dadurch ergibt sich für den Umfang U die Formel: U= a+a+b+b = (2*a)+(2*b).<br /> |
| + | |||
==Formel für den Flächeninhalt== | ==Formel für den Flächeninhalt== | ||
| − | Der Flächeninhalt A eines Rechtecks wird ermittelt, indem man die Länge a mit der Breite b multipliziert. Die Formel lautet: A=a*b. | + | Der Flächeninhalt A eines Rechtecks wird ermittelt, indem man die Länge a mit der Breite b multipliziert. Die Formel lautet: A=a*b.<br /> |
| + | |||
==Symmetrieachsen== | ==Symmetrieachsen== | ||
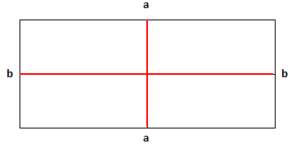
| − | Ein Rechteck hat zwei Symmetrieachsen, die senkrecht aufeinander stehen. Die Symmetrieachsen verlaufen jeweils von der Mitte einer | + | Ein Rechteck hat zwei Symmetrieachsen, die senkrecht aufeinander stehen. Die Symmetrieachsen verlaufen jeweils von der Mitte einer Seite zur Mitte der gegenüberliegenden Seite. Man nennt sie deshalb auch Mittelsenkrechte. Ein Rechteck ist achsensymmetrisch bezüglich dieser Mittelsenkrechten. |
| − | + | [[Datei:Symmetrie.PNG|miniatur|zentriert|Rechteck mit zwei Symmetrieachsen]]<br /> | |
| − | =="Wusstest du schon...?"== | + | |
| + | ==Beziehungen zu anderen Vierecken== | ||
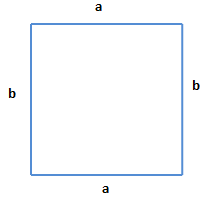
| + | Ein Sonderfall des Rechtecks ist das [[Matheprojekte der Justus-Liebig-Universität Gießen für Grundschülerinnen und Grundschüler/Mathelexikon WiSe 16 17/Quadrat|Quadrat]]. Dies ist dann der Fall, wenn alle vier Seiten eines Rechtecks gleich lang sind.<br /> | ||
| + | [[Datei:Quadrat3.PNG|miniatur|zentriert|Rechteck mit vier gleichlangen Seiten (a=b) = Quadrat]]<br /> | ||
| + | |||
| + | Ein Rechteck ist ein Parallelogramm mit vier rechten Winkeln. Somit ist es eine besondere Form eines Parallelogramms.<br /><br /> | ||
| + | |||
| + | |||
| + | ==="Wusstest du schon...?"=== | ||
Ein perfektes Rechteck ist ein Rechteck, das sich lückenlos und überscheidungsfrei mit Quadraten überdecken lässt. Dabei sind alle verwendeten Quadrate unterschiedlich groß. Es ist gar nicht so leicht, eine solche Zerlegung eines Rechtecks zu finden. Zbigniew Moroń hat das im Jahre 1925 geschafft. Er hat ein Rechteck mit den Seitenlängen a=33 und b=32 in 9 Quadrate mit den Seitenlängen 1, 4, 7, 8, 9, 10, 14, 15 und 18 zerlegt. | Ein perfektes Rechteck ist ein Rechteck, das sich lückenlos und überscheidungsfrei mit Quadraten überdecken lässt. Dabei sind alle verwendeten Quadrate unterschiedlich groß. Es ist gar nicht so leicht, eine solche Zerlegung eines Rechtecks zu finden. Zbigniew Moroń hat das im Jahre 1925 geschafft. Er hat ein Rechteck mit den Seitenlängen a=33 und b=32 in 9 Quadrate mit den Seitenlängen 1, 4, 7, 8, 9, 10, 14, 15 und 18 zerlegt. | ||
[[Datei:Perfektes Rechteck.svg|miniatur|zentriert|Perfektes Rechteck mit der Länge a=33 und der Breite b=32]] | [[Datei:Perfektes Rechteck.svg|miniatur|zentriert|Perfektes Rechteck mit der Länge a=33 und der Breite b=32]] | ||
Aktuelle Version vom 25. Januar 2017, 22:43 Uhr
Inhaltsverzeichnis |
Definition
Ein Rechteck ist eine ebene Figur. Es ist ein Viereck mit parallelen Gegenseiten und vier rechten Winkeln. Die Winkelsumme der Innenwinkel beträgt also 360°. Die gegenüberliegenden Seiten eines Rechtecks sind jeweils gleich lang. Die beiden längeren Seiten bezeichnet man als Länge a des Rechtecks. Die beiden kürzeren Seiten werden als Breite b des Rechtecks bezeichnet. Auch die Diagonalen d in einem Rechteck sind gleich lang und halbieren sich gegenseitig.
Formel für den Umfang
Der Umfang eines Rechtecks lässt sich berechnen, indem man die Seitenlängen aller vier Seiten addiert. Da jeweils zwei Seiten eines Rechtecks gleich lang sind, kann man diese mit „2“ multiplizieren. Dadurch ergibt sich für den Umfang U die Formel: U= a+a+b+b = (2*a)+(2*b).
Formel für den Flächeninhalt
Der Flächeninhalt A eines Rechtecks wird ermittelt, indem man die Länge a mit der Breite b multipliziert. Die Formel lautet: A=a*b.
Symmetrieachsen
Ein Rechteck hat zwei Symmetrieachsen, die senkrecht aufeinander stehen. Die Symmetrieachsen verlaufen jeweils von der Mitte einer Seite zur Mitte der gegenüberliegenden Seite. Man nennt sie deshalb auch Mittelsenkrechte. Ein Rechteck ist achsensymmetrisch bezüglich dieser Mittelsenkrechten.
Beziehungen zu anderen Vierecken
Ein Sonderfall des Rechtecks ist das Quadrat. Dies ist dann der Fall, wenn alle vier Seiten eines Rechtecks gleich lang sind.
Ein Rechteck ist ein Parallelogramm mit vier rechten Winkeln. Somit ist es eine besondere Form eines Parallelogramms.
"Wusstest du schon...?"
Ein perfektes Rechteck ist ein Rechteck, das sich lückenlos und überscheidungsfrei mit Quadraten überdecken lässt. Dabei sind alle verwendeten Quadrate unterschiedlich groß. Es ist gar nicht so leicht, eine solche Zerlegung eines Rechtecks zu finden. Zbigniew Moroń hat das im Jahre 1925 geschafft. Er hat ein Rechteck mit den Seitenlängen a=33 und b=32 in 9 Quadrate mit den Seitenlängen 1, 4, 7, 8, 9, 10, 14, 15 und 18 zerlegt.