Verdoppeln und Halbieren: Unterschied zwischen den Versionen
(→Verdoppeln) |
(→Halbieren) |
||
| (48 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | == Verdoppeln | + | == Verdoppeln und Halbieren == |
| + | Beim Verdoppeln und Halbieren ist die Zahl 2 sehr wichtig. | ||
| + | Sie vergrößert die Ausgangsmenge beim Verdoppeln, während sie beim Halbieren die Ausgangsmenge verkleinert. | ||
| + | Wie das genauer aussieht, wird im Nachfolgenden beschrieben. | ||
| − | + | == Verdoppeln == | |
| − | |||
| − | + | Verdoppeln ist ein Vorgang, bei dem man die Ausgangmenge mit der Zahl 2 multipliziert (mal nimmt). Die neue Menge besteht so aus zweimal der gleichen Ausgangsmenge. | |
| − | |||
| − | |||
| − | + | [[Datei:5x2 neu.PNG|800px|miniatur|zentriert]] | |
| − | |||
| − | + | Es wird die gleiche Menge zu der Ausgangsmenge addiert. | |
| − | Das | + | In diesem Fall werden zu den 5 Äpfeln (Ausgangsmenge) 5 weitere Äpfel dazugenommen. Das ergibt 10 Äpfel, weil 5 + 5 = 10 sind. |
| + | In der Mathematik wird das Addieren der gleichen Menge auch durch das Multiplizieren (Malnehmen) mit 2 ausgedrückt. | ||
| + | Deshalb ist 5 x 2 = 10. | ||
| − | + | Immer wenn man mal 2 multipliziert (mal nimmt) wird die Menge verdoppelt. Multiplizieren (Malnehmen) mit 2 und Verdoppeln meint den selben Vorgang. | |
| − | + | == Halbieren == | |
| − | + | Halbieren ist das Gegenteil von Verdoppeln. Wenn die neue Menge aus dem oberen Beispiel, also 10, halbiert wird, dividiert (teilt) man durch 2. | |
| + | Das bedeutet, man teilt die neue Menge in zwei gleichgroße Mengen auf. Dadurch kommt man wieder auf die Ausgangsmenge 5 zurück, denn 10 : 2 = 5. | ||
| − | Besonders schwierig wird das Halbieren, wenn | + | |
| − | Zumindest ist dies im Zahlenraum | + | [[Datei:10 durch 2 neu.PNG|800px|miniatur|zentriert|Es handelt sich links um die gleiche Menge, die im ersten Beispiel durch den Vorgang des Verdoppelns entstanden ist.]] |
| + | |||
| + | Deswegen ist Dividieren (Teilen) das Gegenteil von Multiplizieren (Malnehmen). | ||
| + | |||
| + | === Halbieren von Ungeraden Zahlen === | ||
| + | |||
| + | Besonders schwierig wird das Halbieren, wenn es sich um eine ungerade Zahl handelt, zum Beispiel 5. Beim Halbieren der 5 soll diese in zwei gleiche Teile zerlegt werden. Doch bei dem Versuch 5 Äpfel in zwei gleich große Teile aufzuteilen, bleibt ein Apfel übrig. Es ist scheinbar nicht möglich 5 zu halbieren. | ||
| + | |||
| + | [[Datei:5 durch 2 neu.PNG|800px|miniatur|zentriert]] | ||
| + | |||
| + | |||
| + | Zumindest ist dies im Zahlenraum, in dem nur ganze Zahlen (1, 2, ...652 usw.) existieren, nicht vorstellbar. | ||
| + | |||
| + | Um dennoch solch eine Rechnung lösen zu können, gibt es die Bruchzahlen. | ||
| + | |||
| + | Im Alltag könnte der Apfel, der bei dem Versuch 5 zu halbieren übrig bleibt, mit einem Messer halbiert werden. | ||
| + | In der Mathematik wird dieser Vorgang durch Bruchzahlen dargestellt. Wenn ein Apfel durchgeschnitten wird, repräsentiert die Bruchzahl ½ die eine Hälfte des Apfels. | ||
| + | |||
| + | [[Datei:5 durch 2 bruch.PNG|800px|miniatur|zentriert|Der durchgeschnittene Apfel wird durch die Zahl ½ ausgedrückt.]] | ||
| + | |||
| + | |||
| + | Die Hälfte von 5 ist deshalb 2 ½ und das Doppelte von 2 ½ ist 5. | ||
Aktuelle Version vom 21. Februar 2017, 21:19 Uhr
Inhaltsverzeichnis |
Verdoppeln und Halbieren
Beim Verdoppeln und Halbieren ist die Zahl 2 sehr wichtig. Sie vergrößert die Ausgangsmenge beim Verdoppeln, während sie beim Halbieren die Ausgangsmenge verkleinert. Wie das genauer aussieht, wird im Nachfolgenden beschrieben.
Verdoppeln
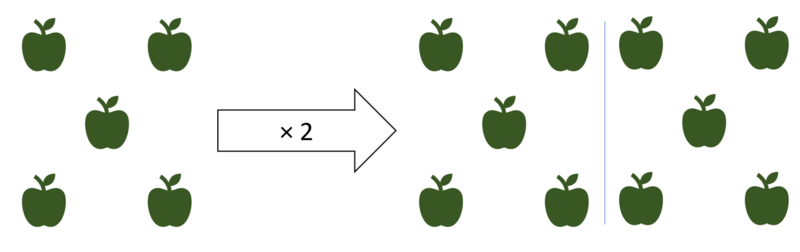
Verdoppeln ist ein Vorgang, bei dem man die Ausgangmenge mit der Zahl 2 multipliziert (mal nimmt). Die neue Menge besteht so aus zweimal der gleichen Ausgangsmenge.
Es wird die gleiche Menge zu der Ausgangsmenge addiert.
In diesem Fall werden zu den 5 Äpfeln (Ausgangsmenge) 5 weitere Äpfel dazugenommen. Das ergibt 10 Äpfel, weil 5 + 5 = 10 sind.
In der Mathematik wird das Addieren der gleichen Menge auch durch das Multiplizieren (Malnehmen) mit 2 ausgedrückt. Deshalb ist 5 x 2 = 10.
Immer wenn man mal 2 multipliziert (mal nimmt) wird die Menge verdoppelt. Multiplizieren (Malnehmen) mit 2 und Verdoppeln meint den selben Vorgang.
Halbieren
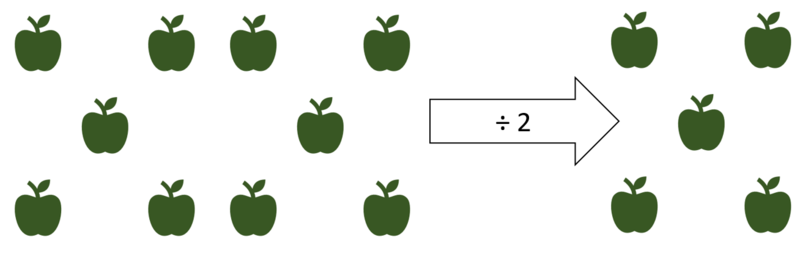
Halbieren ist das Gegenteil von Verdoppeln. Wenn die neue Menge aus dem oberen Beispiel, also 10, halbiert wird, dividiert (teilt) man durch 2. Das bedeutet, man teilt die neue Menge in zwei gleichgroße Mengen auf. Dadurch kommt man wieder auf die Ausgangsmenge 5 zurück, denn 10 : 2 = 5.
Deswegen ist Dividieren (Teilen) das Gegenteil von Multiplizieren (Malnehmen).
Halbieren von Ungeraden Zahlen
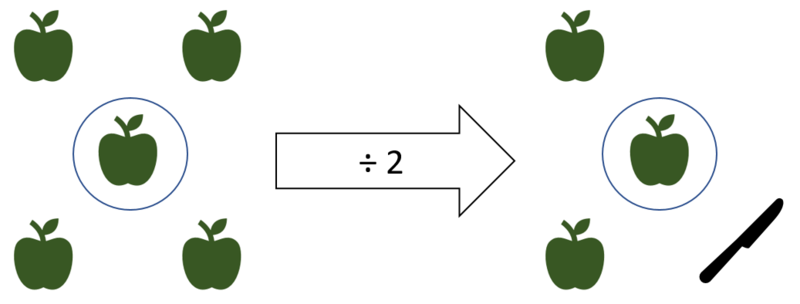
Besonders schwierig wird das Halbieren, wenn es sich um eine ungerade Zahl handelt, zum Beispiel 5. Beim Halbieren der 5 soll diese in zwei gleiche Teile zerlegt werden. Doch bei dem Versuch 5 Äpfel in zwei gleich große Teile aufzuteilen, bleibt ein Apfel übrig. Es ist scheinbar nicht möglich 5 zu halbieren.
Zumindest ist dies im Zahlenraum, in dem nur ganze Zahlen (1, 2, ...652 usw.) existieren, nicht vorstellbar.
Um dennoch solch eine Rechnung lösen zu können, gibt es die Bruchzahlen.
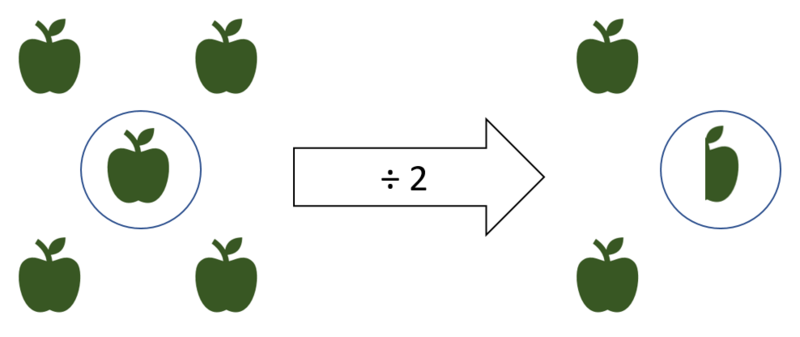
Im Alltag könnte der Apfel, der bei dem Versuch 5 zu halbieren übrig bleibt, mit einem Messer halbiert werden. In der Mathematik wird dieser Vorgang durch Bruchzahlen dargestellt. Wenn ein Apfel durchgeschnitten wird, repräsentiert die Bruchzahl ½ die eine Hälfte des Apfels.
Die Hälfte von 5 ist deshalb 2 ½ und das Doppelte von 2 ½ ist 5.