Umfang: Unterschied zwischen den Versionen
| (7 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 5: | Zeile 5: | ||
Der Umfang beschreibt im Allgemeinen die Länge der Außenlinie die eine Form, einen Gegenstand oder <br /> | Der Umfang beschreibt im Allgemeinen die Länge der Außenlinie die eine Form, einen Gegenstand oder <br /> | ||
eine mathematische Figur umfasst.<br /> | eine mathematische Figur umfasst.<br /> | ||
| − | + | <br /> | |
| − | Legt man ein Maßband um | + | Der Umfang lässt sich durch Messen bestimmen.<br /> |
| − | + | <br /> | |
| + | Legt man ein Maßband beispielsweise um eine Dose und liest an der Messskala 25 cm ab, so beträgt der Umfang der Dose an dieser Stelle 25cm. | ||
<br /> | <br /> | ||
<br /> | <br /> | ||
| Zeile 15: | Zeile 16: | ||
== '''Der Umfang in der Mathematik''' == | == '''Der Umfang in der Mathematik''' == | ||
| − | + | In der Mathematik wird der Umfang von Gegenständen oder Figuren meist berechnet, da das reine Messen von diesem nicht immer ganz genau ist. | |
=== '''Umfangsberechnung von Vielecken''' === | === '''Umfangsberechnung von Vielecken''' === | ||
| − | + | <br /> | |
| − | Ein Vieleck ist eine | + | Ein Vieleck ist eine aus Seiten und Punkten bestehende Figur. |
| − | + | Es besteht aus mindestens drei Punkten, welche durch die Seiten miteinander verbunden sind und somit eine geschlossene Figur bilden.<br /> | |
| − | + | Zu den am häufigsten verwendeten Vielecken gehören zum Beispiel das Dreieck, welches aus drei durch Seiten miteinander verbundenen Punkten/Ecken besteht, sowie die Vierecke Rechteck und Quadrat, welche aus jeweils vier Punkten und Seiten bestehen.<br /> | |
| − | Zu den am häufigsten verwendeten Vielecken gehören zum Beispiel das Dreieck, welches aus drei durch Seiten miteinander verbundenen Punkten/Ecken besteht, sowie | + | |
| − | + | ||
Für die Berechnung des Umfangs eines Vielecks muss man die Länge aller Seiten kennen und diese Seitenlängen dann addieren.<br /> | Für die Berechnung des Umfangs eines Vielecks muss man die Länge aller Seiten kennen und diese Seitenlängen dann addieren.<br /> | ||
| − | + | '''Die Summe aller Seitenlängen ergibt den Umfang.'''<br /> | |
| − | '''Die Summe aller Seitenlängen ergibt | + | <br /> |
| − | + | ||
| − | + | ||
Für die Berechnung des Umfangs von Vielecken gibt es Formeln, welche alle auf der Addition aller Seitenlängen basieren. | Für die Berechnung des Umfangs von Vielecken gibt es Formeln, welche alle auf der Addition aller Seitenlängen basieren. | ||
| − | + | <br /> | |
| + | <br /> | ||
| + | <br /> | ||
| + | <br /> | ||
==== '''Umfangsberechnung Dreieck''' ==== | ==== '''Umfangsberechnung Dreieck''' ==== | ||
[[Datei:Umfang Dreieck NEU.png|thumb||220px|right]] | [[Datei:Umfang Dreieck NEU.png|thumb||220px|right]] | ||
<br /> | <br /> | ||
| + | Ein Dreieck besteht aus den drei Seiten a, b und c, dessen Längen unterschiedlich sein können, aber nicht müssen. Den Umfang eines Dreiecks berechnet man indem man die Länge der drei Seiten a, b und c addiert. <br /> | ||
<br /> | <br /> | ||
| − | + | So ergibt sich folgende Formel für den Umfang des Dreiecks:<br /> | |
| − | + | ||
| − | So ergibt sich folgende Formel:<br /> | + | |
<br /> | <br /> | ||
Umfang (U) = '''a + b + c'''<br /> | Umfang (U) = '''a + b + c'''<br /> | ||
| Zeile 51: | Zeile 50: | ||
[[Datei:Umfang Rechteck.png|thumb||270px|right]] | [[Datei:Umfang Rechteck.png|thumb||270px|right]] | ||
<br /> | <br /> | ||
| + | Ein [[Matheprojekte der Justus-Liebig-Universität Gießen für Grundschülerinnen und Grundschüler/Mathelexikon WiSe 16 17/Rechteck|Rechteck]] besteht aus vier Seiten, von denen jeweils die zwei gegenüberliegenden Seiten die selbe Länge haben. Diese Seiten sind mit a und b gekennzeichnet. Den Umfang eines Rechtecks berechnet man indem man zwei Mal die Länge der Seite a mit zwei Mal der Länge der Seite b addiert.<br /> | ||
<br /> | <br /> | ||
| − | + | So ergibt sich folgende Formel für den Umfang des Rechtecks:<br /> | |
| − | + | ||
| − | So ergibt sich folgende Formel:<br /> | + | |
<br /> | <br /> | ||
Umfang (U) = a + a + b + b <br /> | Umfang (U) = a + a + b + b <br /> | ||
| Zeile 65: | Zeile 63: | ||
[[Datei:Umfang Quadrat.png|thumb||250px|right]] | [[Datei:Umfang Quadrat.png|thumb||250px|right]] | ||
| − | + | <br /> | |
| − | + | Ein [[Matheprojekte der Justus-Liebig-Universität Gießen für Grundschülerinnen und Grundschüler/Mathelexikon WiSe 16 17/Quadrat|Quadrat]] besteht aus vier Seiten. Alle Seiten haben die selbe Länge, weshalb sie alle mit a gekennzeichnet sind. Den Umfang eines Quadrats berechnet man indem man vier Mal die Länge der Seite a addiert.<br /> | |
| − | [[Matheprojekte der Justus-Liebig-Universität Gießen für Grundschülerinnen und Grundschüler/Mathelexikon WiSe 16 17/Quadrat|Quadrat]] | + | <br /> |
| − | + | So ergibt sich folgende Formel für den Umfang des Quadrats:<br /> | |
| + | <br /> | ||
Umfang (U) = a + a + a + a<br /> | Umfang (U) = a + a + a + a<br /> | ||
'''= 4 x a''' | '''= 4 x a''' | ||
| Zeile 79: | Zeile 78: | ||
[[Datei:Umfang Vieleck.png|thumb||right|220px]] | [[Datei:Umfang Vieleck.png|thumb||right|220px]] | ||
| − | + | <br /> | |
| − | Es gibt natürlich noch viele weitere Vielecke. Die Berechnung des Umfangs ist aber immer die selbe. | + | Es gibt natürlich noch viele weitere Vielecke. Die Berechnung des Umfangs ist aber immer die selbe. Man addiert immer die Länge aller vorhandenen Seiten um den Umfang jedes beliebigen Vielecks zu erhalten. Hier wird beispielsweise die Umfangsberechnung eines Sechsecks dargestellt.<br /> |
| − | + | <br /> | |
| − | + | So ergibt sich folgende Formel für den Umfang dieses Vielecks:<br /> | |
| + | <br /> | ||
Umfang (U) = '''a + b + c + d + e + f''' | Umfang (U) = '''a + b + c + d + e + f''' | ||
Aktuelle Version vom 1. März 2017, 15:18 Uhr
Inhaltsverzeichnis |
Der Umfang allgemein
Der Umfang beschreibt im Allgemeinen die Länge der Außenlinie die eine Form, einen Gegenstand oder
eine mathematische Figur umfasst.
Der Umfang lässt sich durch Messen bestimmen.
Legt man ein Maßband beispielsweise um eine Dose und liest an der Messskala 25 cm ab, so beträgt der Umfang der Dose an dieser Stelle 25cm.
Der Umfang in der Mathematik
In der Mathematik wird der Umfang von Gegenständen oder Figuren meist berechnet, da das reine Messen von diesem nicht immer ganz genau ist.
Umfangsberechnung von Vielecken
Ein Vieleck ist eine aus Seiten und Punkten bestehende Figur.
Es besteht aus mindestens drei Punkten, welche durch die Seiten miteinander verbunden sind und somit eine geschlossene Figur bilden.
Zu den am häufigsten verwendeten Vielecken gehören zum Beispiel das Dreieck, welches aus drei durch Seiten miteinander verbundenen Punkten/Ecken besteht, sowie die Vierecke Rechteck und Quadrat, welche aus jeweils vier Punkten und Seiten bestehen.
Für die Berechnung des Umfangs eines Vielecks muss man die Länge aller Seiten kennen und diese Seitenlängen dann addieren.
Die Summe aller Seitenlängen ergibt den Umfang.
Für die Berechnung des Umfangs von Vielecken gibt es Formeln, welche alle auf der Addition aller Seitenlängen basieren.
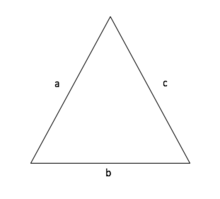
Umfangsberechnung Dreieck
Ein Dreieck besteht aus den drei Seiten a, b und c, dessen Längen unterschiedlich sein können, aber nicht müssen. Den Umfang eines Dreiecks berechnet man indem man die Länge der drei Seiten a, b und c addiert.
So ergibt sich folgende Formel für den Umfang des Dreiecks:
Umfang (U) = a + b + c
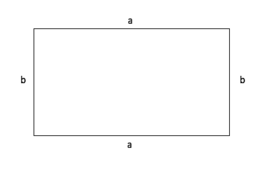
Umfangsberechnung Rechteck
Ein Rechteck besteht aus vier Seiten, von denen jeweils die zwei gegenüberliegenden Seiten die selbe Länge haben. Diese Seiten sind mit a und b gekennzeichnet. Den Umfang eines Rechtecks berechnet man indem man zwei Mal die Länge der Seite a mit zwei Mal der Länge der Seite b addiert.
So ergibt sich folgende Formel für den Umfang des Rechtecks:
Umfang (U) = a + a + b + b
= 2 x a + 2 x b
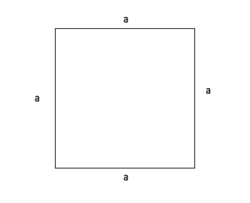
Umfangsberechnung Quadrat
Ein Quadrat besteht aus vier Seiten. Alle Seiten haben die selbe Länge, weshalb sie alle mit a gekennzeichnet sind. Den Umfang eines Quadrats berechnet man indem man vier Mal die Länge der Seite a addiert.
So ergibt sich folgende Formel für den Umfang des Quadrats:
Umfang (U) = a + a + a + a
= 4 x a
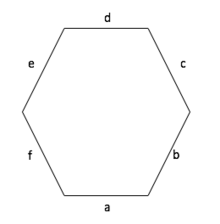
Umfangsberechnung beliebiges Vieleck
Es gibt natürlich noch viele weitere Vielecke. Die Berechnung des Umfangs ist aber immer die selbe. Man addiert immer die Länge aller vorhandenen Seiten um den Umfang jedes beliebigen Vielecks zu erhalten. Hier wird beispielsweise die Umfangsberechnung eines Sechsecks dargestellt.
So ergibt sich folgende Formel für den Umfang dieses Vielecks:
Umfang (U) = a + b + c + d + e + f