Drachen: Unterschied zwischen den Versionen
Aus Grundschullernportal
< Matheprojekte der Justus-Liebig-Universität Gießen für Grundschülerinnen und Grundschüler | Mathelexikon WiSe 16 17
| Zeile 4: | Zeile 4: | ||
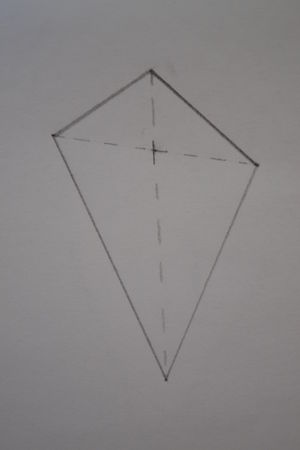
Der schiefe Drachen ist ein Viereck bei dem eine Diagonale (Diagonale = die Verbindung von zwei gegenüberliegenden Ecken) von der anderen halbiert wird. | Der schiefe Drachen ist ein Viereck bei dem eine Diagonale (Diagonale = die Verbindung von zwei gegenüberliegenden Ecken) von der anderen halbiert wird. | ||
| + | |||
| + | [[Datei:Schiefer Drachen.JPG|thumb|Bild eines schiefen Drachens]] | ||
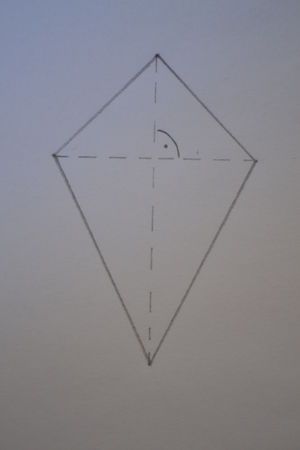
Der symmetrische Drachen ist ein Drachen, der achsensymmetrisch ist. Außerdem hat er folgende Eigenschaften: | Der symmetrische Drachen ist ein Drachen, der achsensymmetrisch ist. Außerdem hat er folgende Eigenschaften: | ||
| Zeile 10: | Zeile 12: | ||
* es gibt zwei Paar gleich lange benachbarte Seiten | * es gibt zwei Paar gleich lange benachbarte Seiten | ||
* es gibt ein Paar gleich große gegenüberliegende Winkel | * es gibt ein Paar gleich große gegenüberliegende Winkel | ||
| + | |||
| + | [[Datei:Symmetrischer Drachen.JPG|thumb|Bild eines symmetrischen Drachens]] | ||
Die Raute ist auch ein symmetrischer Drachen, bei dem alle Seiten gleich lang sind. | Die Raute ist auch ein symmetrischer Drachen, bei dem alle Seiten gleich lang sind. | ||
Version vom 17. Januar 2017, 16:23 Uhr
Der Drachen ist ein besonderes Viereck.
Man kann zwischen dem schiefen/schrägen Drachen und dem symmetrischen Drachen unterscheiden.
Der schiefe Drachen ist ein Viereck bei dem eine Diagonale (Diagonale = die Verbindung von zwei gegenüberliegenden Ecken) von der anderen halbiert wird.
Der symmetrische Drachen ist ein Drachen, der achsensymmetrisch ist. Außerdem hat er folgende Eigenschaften:
- eine Diagonale wird von der anderen halbiert (wie beim schiefen/schrägen Drachen)
- die Diagonalen stehen senkrecht aufeinander
- es gibt zwei Paar gleich lange benachbarte Seiten
- es gibt ein Paar gleich große gegenüberliegende Winkel
Die Raute ist auch ein symmetrischer Drachen, bei dem alle Seiten gleich lang sind.