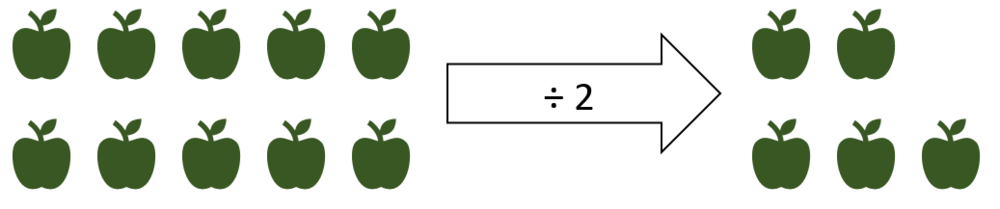Verdoppeln und Halbieren: Unterschied zwischen den Versionen
(→Verdoppeln) |
(→Verdoppeln) |
||
| Zeile 6: | Zeile 6: | ||
== Verdoppeln == | == Verdoppeln == | ||
| − | Verdoppeln ist ein mathematischer Vorgang, | + | |
| + | Verdoppeln ist ein mathematischer Vorgang, bei dem man die Ausgangmenge mit der Zahl zwei multipliziert (malnimmt). Die neue Menge besteht so aus zweimal der gleichen Ausgangsmenge. | ||
| + | |||
[[Datei:5 mal 2.PNG|1000px|miniatur|zentriert]] | [[Datei:5 mal 2.PNG|1000px|miniatur|zentriert]] | ||
Version vom 17. Januar 2017, 20:10 Uhr
Inhaltsverzeichnis |
Verdoppeln und Halbieren
Beim Verdoppeln und Halbieren wird immer mit der Zahl Zwei gearbeitet. Sie unterscheiden sich jedoch darin, wie die Zwei auf Mengen wirkt. Beim Verdoppeln wird die Ausgangsmenge größer, beim Halbieren dagegen wird die Ausgansmenge kleiner. Wie das genauer funktioniert, wird im Nachfolgenden beschrieben.
Verdoppeln
Verdoppeln ist ein mathematischer Vorgang, bei dem man die Ausgangmenge mit der Zahl zwei multipliziert (malnimmt). Die neue Menge besteht so aus zweimal der gleichen Ausgangsmenge.
Es wird die gleiche Menge zu der Ausgangsmenge dazu genommen. In diesem Fall 5 zu der 5 = 10, weil 5 + 5 = 10. In der Mathematik wird der das dazuziehen der gleichen Menge auch durch das Zwei malnehmen ausgedrückt. Deshalb 5 x 2 = 10.
Immer wenn man mal 2 nimmt wird die Menge verdoppelt. Mal zwei und verdoppeln meint den selben Vorgang.
Halbieren
Halbieren entspricht dem Gegenteil von verdoppeln. Wenn die neue Menge aus dem oberen Beispiel, also 10, halbiert wird, teilen wir durch 2. Das bedeutet, wir teilen die neue Menge in zwei gleichgroße Mengen auf. Dadurch kommt man wieder auf die Ausgangsmenge 5 zurück, denn 10 : 2 = 5.
Deswegen ist teilen, oder auch dividieren genannt, das Gegenteil von multiplizieren.
Halbieren durch Ungerade Zahlen
Besonders schwierig wird das Halbieren, wenn wir eine ungerade Zahl haben, z.B. die 5. Da beim Halbieren die Ausgangsmenge in zwei gleiche Teile zerlegt werden soll, ist das mit der 5 scheinbar nicht möglich.
Zumindest ist dies im Zahlenraum Z , in dem nur ganze Zahlen existieren, nicht vorstellbar. Um dennoch solch eine Rechnung lösen zu können, gibt es die Bruchzahlen, die den Zahlenraum Q bilden. Wenn ein Apfel durchgeschnitten wird, stellt die Hälft sozusagen eine Bruchzahl dar 1/2.
Deshalb ist 5 halbiert 2 1/2 und 2 1/2 verdoppelt 5.